I like the idea of folding the triangle down so that all angles are in a straight line to be useful.
Today the main problem is:
Types of angles
Acute angle:
An angle whose measure is less than 90 degrees. The following is an acute angle.
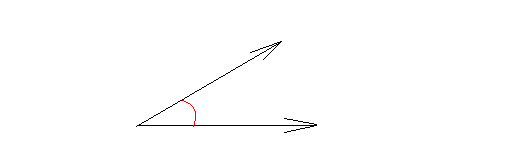
Right angle:
An angle whose measure is 90 degrees. The following is a right angle.
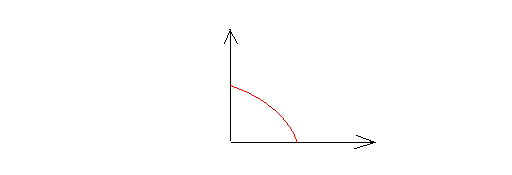
Obtuse angle:
An angle whose measure is bigger than 90 degrees but less than 180 degrees. Thus, it is between 90 degrees and 180 degrees. The following is an obtuse angle.
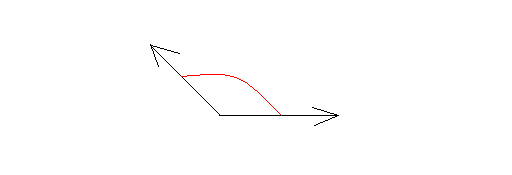
Straight angle
An angle whose measure is 180 degrees.Thus, a straight angle look like a straight line. The following is a straight angle.
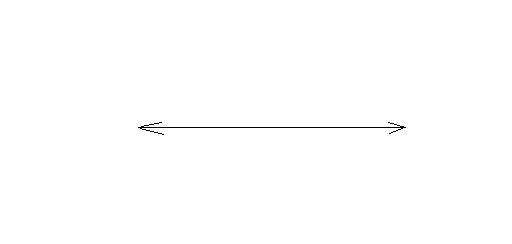
Reflex angle:
An angle whose measure is bigger than 180 degrees but less than 360 degrees.The following is a reflex angle.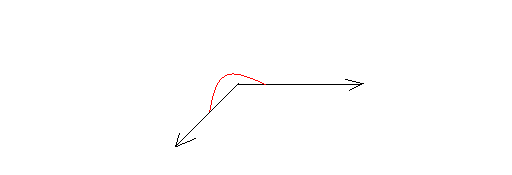
Adjacent angles:
Angle with a common vertex and one common side. <1 and <2, are adjacent angles.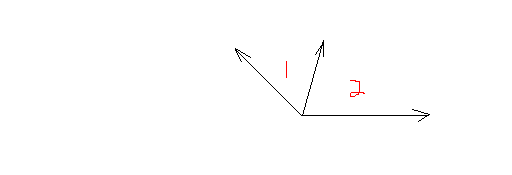
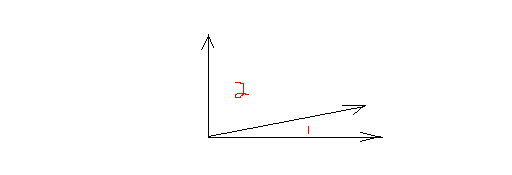
Complementary angles:
Two angles whose measures add to 90 degrees. Angle 1 and angle 2 are complementary angles because together they form a right angle.
Note that angle 1 and angle 2 do not have to be adjacent to be complementary as long as they add up to 90 degrees
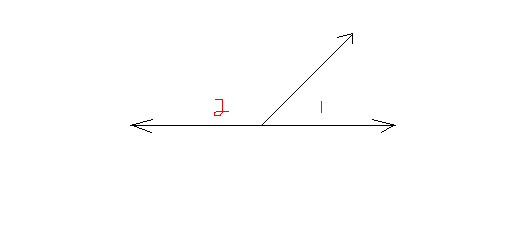
Supplementary angles:
Two angles whose measures add to 180 degrees. The following are supplementary angles.
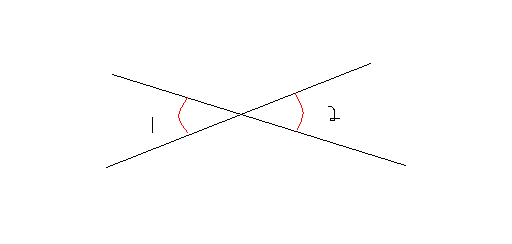
Vertical angles:
Angles that have a common vertex and whose sides are formed by the same lines. The following(angle 1 and angle 2) are vertical angles.
When two parallel lines are crossed by a third line(Transversal), 8 angles are formed. Take a look at the following figure
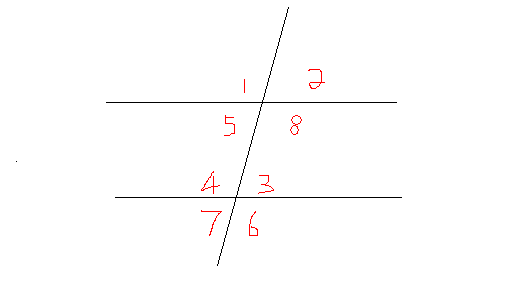
Angles 3,4,5,8 are interior angles
Angles 1,2,6,7 are exterior angles
Alternate interior angles:
Pairs of interior angles on opposite sides of the transversal.
For instance, angle 3 and angle 5 are alternate interior angles. Angle 4 and angle 8 are also alternate interior angles.
Alternate exterior angles:
Pairs of exterior angles on opposite sides of the transversal.
Angle 2 and angle 7 are alternate exterior angles.
Corresponding angles:
Pairs of angles that are in similar positions.
Angle 3 and angle 2 are corresponding angles.
Angle 5 and angle 7 are corresponding angles
An angle whose measure is less than 90 degrees. The following is an acute angle.

Right angle:
An angle whose measure is 90 degrees. The following is a right angle.

Obtuse angle:
An angle whose measure is bigger than 90 degrees but less than 180 degrees. Thus, it is between 90 degrees and 180 degrees. The following is an obtuse angle.

Straight angle
An angle whose measure is 180 degrees.Thus, a straight angle look like a straight line. The following is a straight angle.

Reflex angle:
An angle whose measure is bigger than 180 degrees but less than 360 degrees.The following is a reflex angle.

Adjacent angles:
Angle with a common vertex and one common side. <1 and <2, are adjacent angles.

Complementary angles:
Two angles whose measures add to 90 degrees. Angle 1 and angle 2 are complementary angles because together they form a right angle.
Note that angle 1 and angle 2 do not have to be adjacent to be complementary as long as they add up to 90 degrees

Supplementary angles:
Two angles whose measures add to 180 degrees. The following are supplementary angles.

Vertical angles:
Angles that have a common vertex and whose sides are formed by the same lines. The following(angle 1 and angle 2) are vertical angles.

When two parallel lines are crossed by a third line(Transversal), 8 angles are formed. Take a look at the following figure

Angles 3,4,5,8 are interior angles
Angles 1,2,6,7 are exterior angles
Alternate interior angles:
Pairs of interior angles on opposite sides of the transversal.
For instance, angle 3 and angle 5 are alternate interior angles. Angle 4 and angle 8 are also alternate interior angles.
Alternate exterior angles:
Pairs of exterior angles on opposite sides of the transversal.
Angle 2 and angle 7 are alternate exterior angles.
Corresponding angles:
Pairs of angles that are in similar positions.
Angle 3 and angle 2 are corresponding angles.
Angle 5 and angle 7 are corresponding angles

No comments:
Post a Comment